同符号の数の加法

いきなり「加法(かほう)」という，聞きなれない言葉が出てきましたが，加法とは単に足し算のことです。難しそうだと身構える必要はありません。

そして，加法(足し算)の結果のことを「和(わ)」と言います。

\(2+3=5\)とは，\((+2)+(+3)=(+5)\)と同じですから，正の数同士の加法は小学校で習った通りとなります。

では，負の数の加法はどうなるのでしょうか。

例として，\((-2)+(-3)\)について考えます。

負の数同士の加法の結果は，足す数の絶対値の和に\(-\)をつけた数となります。

先ほどの例で見てみると，\(-2\)と\(-3\)の絶対値はそれぞれ\(2\)と\(3\)で，その和は\(2+3=5\)です。よって\((-2)+(-3)=-5\)となります。

途中経過を式で分かりやすく書くと，
\((-2)+(-3)=-(2+3)=-5\)となります。

ここで先ほどの正の数の加法についても同様に
\((+2)+(+3)=+(2+3)=+5\)とできることから，同符号の数の加法は次のようにまとめることができます。

同符号の2つの数の和は絶対値の和に，足す数に共通している符号をつける。

※式の中で\((-2)+(-3)\)のように，\(()\)をどうしてつけているのか気になった人もいると思います。ここで，\((-2)\)としているのは\(-2\)が一つの数であることをわかりやすくするためです。

仮に\(()\)を外して\(-2+-3\)と書いてしまうと，特に左から2番目の\(-\)が引き算を表す\(-\)なのか，「\(-3\)」という数の表記の一部なのか分かりにくくなってしまいます。ひとまずは\(()\)をつけておきましょう。

異符号の数の加法

異符号の数の和については次の2つのSTEPで求めます。

STEP1:足す2つの数の絶対値を比べます。

STEP2:絶対値が等しいときは答えが\(0\)になります。
    :絶対値が等しくないときは，その絶対値の「差」に，足す2つの数のうち絶対値の大きい方の符号を付けます。

具体例を通して理解していきましょう。

\((-3)+(+3)\)という足し算は足す2つの数の絶対値が等しいので，\((-3)+(+3)=0\)となります。

ここで正負の数とはで解説したように，\(-\)は「反対」の意味を表すことを思い出してください。

すると\(-3\)は\(+3\)とちょうど反対の数なので，打ち消しあって答えが\(0\)になるのは直感的に理解しやすいですね。

次に，\((-5)+(+3)\)のような絶対値が等しくない場合について考えていきましょう。

まずSTEP1です。\(-5,+3\)の絶対値はそれぞれ\(5,3\)で，\(5\gt3\)となり\(-5\)の方が絶対値が大きいことがわかります。

そしてSTEP2ですが，STEP2に入る前に，STEP2では「差」という聞きなれない言葉が出てきているので，この言葉の意味から確認していきます。

「差」とは，簡単に言えば，大きい数から小さい数を引いた結果のことを指します。

そのため，「\(5\)と\(3\)の差は？」と聞かれたら，\(5>3\)で，\(5-3=2\)ですから，答えは\(2\)となります。

差の意味が確認できたところで，先ほどの例に立ち返りましょう。\(-5,+3\)の絶対値はそれぞれ\(5,3\)であるので，絶対値の差は\(5-3=2\)ですね。

この\(2\)が「足す2つの数の絶対値の差」に当たりますね。

また，\(5\gt3\)で\(-5\)の方が\(+3\)よりも絶対値が大きいので，「足す2つの数のうちの絶対値の大きい方の符号」は\(-\)となります。

以上より，\(2\)に\(-\)を付けてできた\(-2\)が\((-5)+(+3)\)の答えとなります。

つまり，\((-5)+(+3)=-2\)です。

1. 足す2つの数の絶対値を比べる。
2. 絶対値が等しいか等しくないかで場合分け
   • 等しいとき\(\to\)答えは\(0\)
   • 等しくないとき\(\to\)絶対値の「差」に，足す2つの数のうち絶対値の大きい方の符号を付ける。

このサイトの例題などの演習を通して，異符号の数の加法がスラスラとできるようになっておきましょう。

※ここでは「差」の意味を「大きい数から小さい数を引いた結果」としましたが，「差」は他の意味で使われるときもあります。

\(0\)との加法

\(0\)は正の数でも負の数でもないので，\(0\)との加法はどうするのでしょうか。

\((+3)+0=+3\)のように，正の数に\(0\)を足しても結果は元の正の数のままということはもう知っているかと思います。

実はこれと同様のことが負の数に関しても言えます。つまり\((-1)+0=-1\)のように，負の数に\(0\)を足しても結果は元の負の数のままということですね。

「\(0\)」はよく「無」を表すといわれ，「\(0\)を足す」，すなわち「無を足す」ということが元の数を変えないというのは直感的にわかりやすいですね。

加法の交換法則・結合法則

この次の項目では加法の計算を楽にする工夫を習っていきます。

しかしその前に，その工夫のもととなる加法の法則について知っておく必要があります。

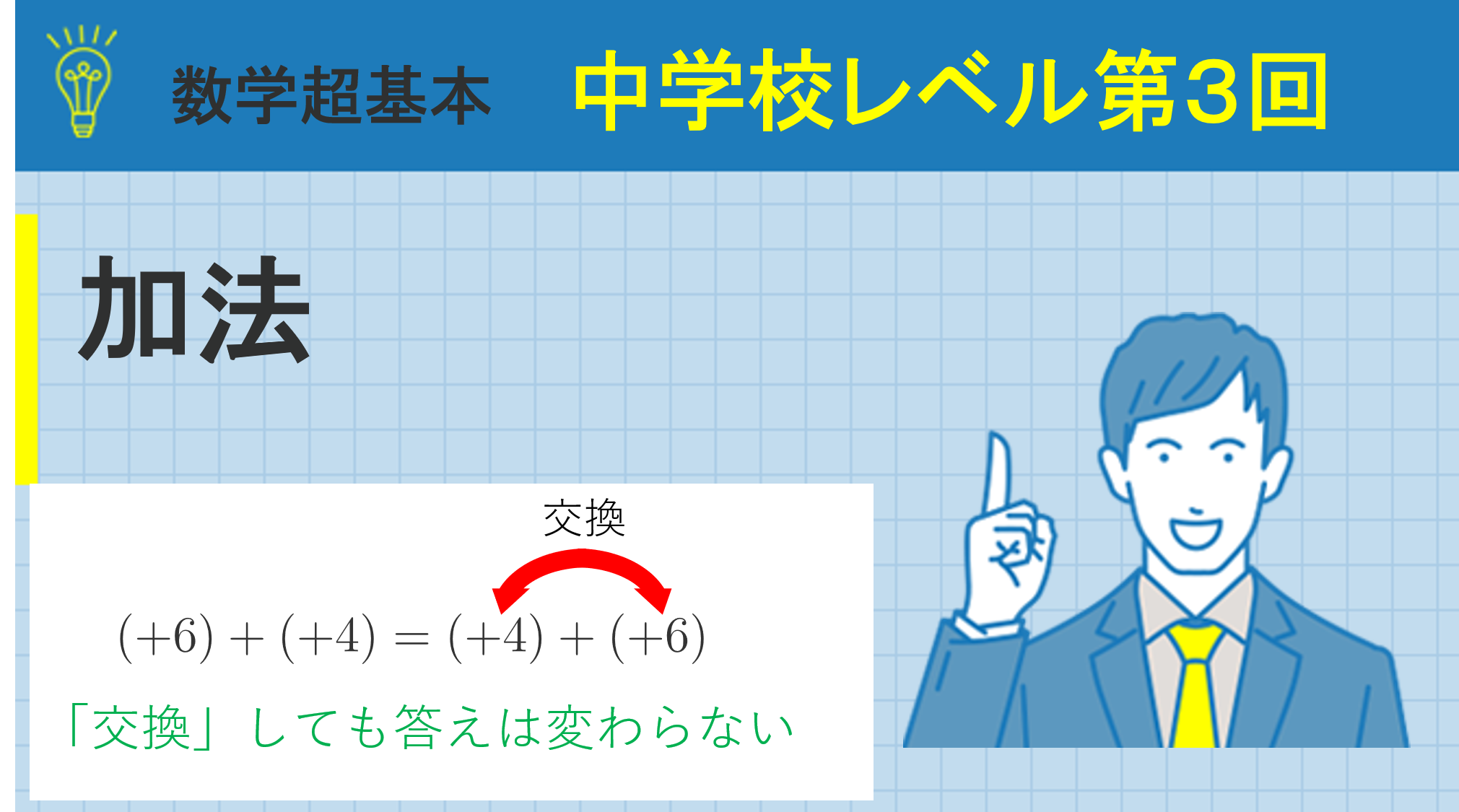
今まで行ってきた正の数の加法では\((+4)+(+6)=(+6)+(+4)\)のように前後の数の順序を入れ替えても答えが変わらないという法則が成り立っていました。

これを加法の交換法則と言います。

また\(\{(+9)+(+3)\}+(+7)=(+9)+\{(+3)+(+7)\}\)のように，式の足し算をどこから計算しても答えが変わらないという法則も成り立っています。

これを加法の結合法則と言います。

※\(\{\}\)は本当は\(()\)と書きたいところを，\(\{\}\)の中にある\(()\)と区別をつけるために書かれるものです。\(()\)の中の式から計算していくので計算順序は下の図のようになります。

そして，交換法則・結合法則は負の数を含めた正負の数の加法でも成り立ちます。

このような法則を聞くと，当たり前のことだと思ってしまうかもしれません。

しかし割り算では\(4\div2=2,\) \(2\div4=\,\dfrac{1}{2}\)で，\(4\div2\neq2\div4\)となるのように交換法則が成り立たないことがわかります。

このように交換法則・結合法則が成り立たない計算もあるので，実はこれらの法則が成り立つことは意外と当たり前ではないのです。

私たちが普段足し算を行っているときには，交換法則・結合法則をあまり意識することなく計算を行う場合がほとんどですが，次の項目で習う加法の工夫はこれらの法則があるからこそできるものです。

つまり，交換法則・結合法則は加法の計算を楽にしてくれる縁の下の力持ちということなので，忘れないようにしておきましょう。

加法の工夫

加法の基本法則が分かったところで，加法の工夫を学んでいきましょう。

\((-1)+(+2)+(-5)+(-6)+(+3)+(+5)\)という複数の数の加法を考えましょう。

一つ目の工夫として，足すことで\(0\)を作れるような数の組がないかを探しましょう。

\(0\)は1-3. \(0\)との加法で習ったように、\(0\)は足した相手の数を変えないことから，計算が非常に楽になるからです。

今回の例では\(+5,-5\)というペアの数がありますね。

よって，そのペア内で数を足して，\((+5)+(-5)=0\)というように\(0\)を作ってしまいましょう。

ここまでの過程は下に示すようになります。

慣れてくると\(+3,+2,-5\)のような，すべて足すと\(0\)になる3つ以上の数の組も見つけることができるようになります。

計算が楽になるよう，できるだけ多くの数を使って\(0\)を作るように心がけましょう。

ただし\(0\)を作る組を探しすぎると，普通に計算するよりもかえって時間がかかってしまいますので，式を一目見て\(0\)を作る組が目につかなかったら次の工夫に移るのがいいでしょう。

二つ目の工夫は，正の数，負の数を集めて，それぞれの数同士で計算することです。

一つ目の工夫をやり終えた後の式は\((-1)+(+2)+(-6)+(+3)\)となっており，この加法内に出てくる数は\(-1,+2,-6,+3\)ですね。

このうち正の数は\(+2,+3\)，負の数は\(-1,-6\)ですから，これら同士を集めて計算します。

そうして計算を続けて行き，下に示すように答えを求めます。

もしこの工夫を行わず，普通に式の左の数から順に計算をしていくと「異符号の数の加法，同符号の数の加法，異符号…」と足す数の符号の違いをいちいち気にしなければならない場合があります。

一方先ほどの工夫では，1-1. 同符号の数の加法で習ったことから，正の数\(+\)正の数\(=\)正の数，負の数\(+\)負の数\(=\)負の数というなることがわかるので，グループ内での足し算は必ず同符号の加法，最後にグループ同士を足す計算では異符号の加法となります。

これなら，いちいち足す数の符号の違いをそれほど意識する必要はないですね。

ところで途中の説明で加法内に出てくる数を調べましたよね。

この加法内に出てくる一つ一つの数のことを項といい，正の数の項は正の項，負の数の項は負の項と言います。

二つ目の工夫をこれらの用語を使ってまとめると，正の項，負の項に分けてそれぞれで計算するということになります。

ここまでで加法の工夫を一通り説明しました。これらの工夫は，あくまで工夫なので絶対にこの工夫を行う必要はありませんが，計算が楽になるので私はオススメします。

この他にも自分にとって計算しやすい工夫を発見したら，それを三つ目，四つ目の工夫として実践していってください。

• 足すことで\(0\)を作れるような数の組がないかを探す
• 正の項，負の項に分けてそれぞれで計算