【超基本_中学校レベル第2回】絶対値 正負の数の大小
こんにちは!半沢です!
この記事は数学超基本シリーズの中学校レベル第2回です。
高校生の皆様には簡単な内容ですが復習のつもりで読んでいただけると幸いです。
中学1年生の数学で習う絶対値から正負の数の大小に関する例題を解説します。
目次
絶対値とは
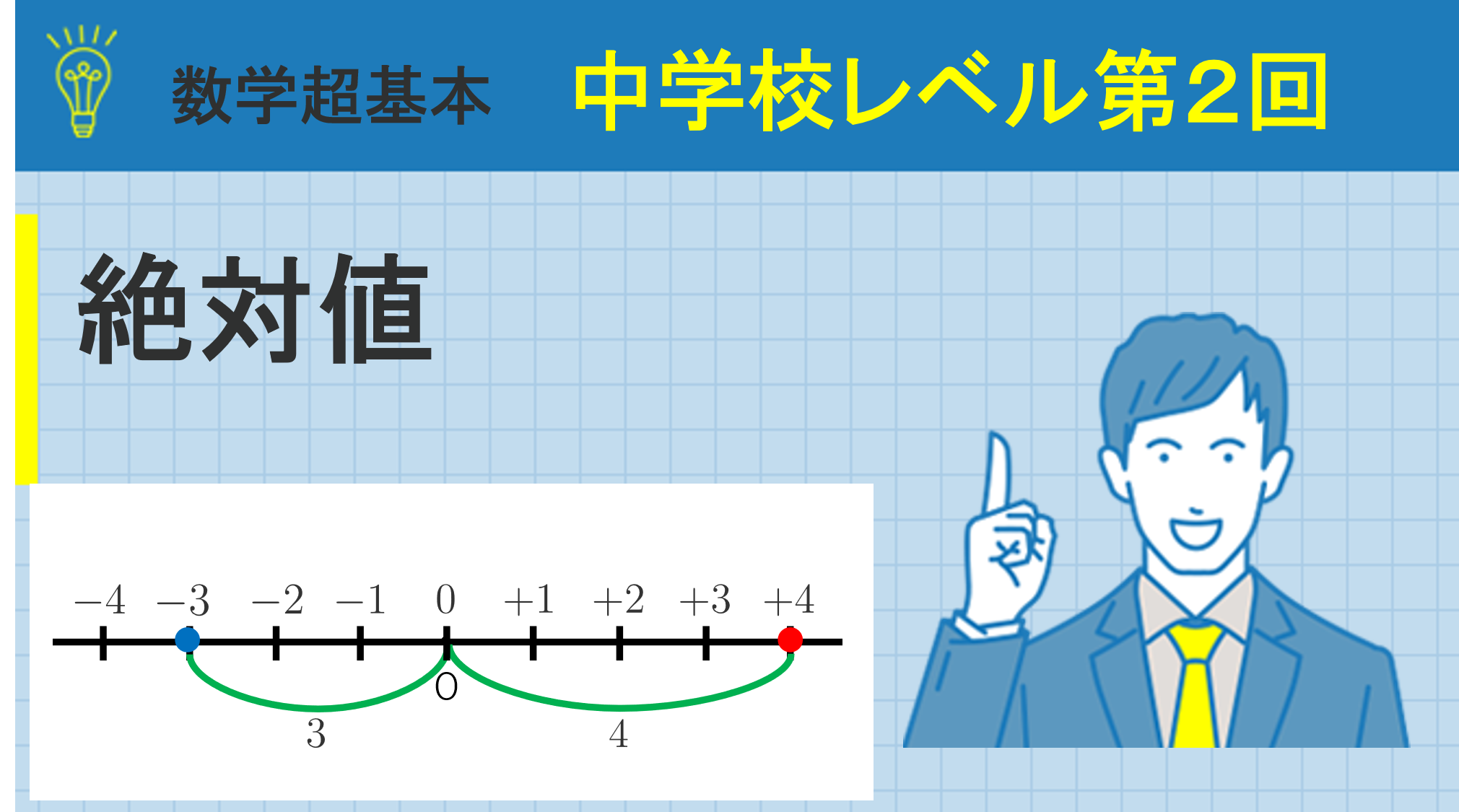
絶対値とは,数直線上での「原点との距離」
見出しにも書いているように,絶対値とは数直線上での「原点(\(0\)に対応する点)との距離」のことです。
具体例を通して理解していきましょう。
「\(+4\)の絶対値は?」と聞かれたら,上の数直線を見ると,\(+4\)の点と原点との距離は\(4\)であることがわかるので,答えは\(4\)となります。
負の数の絶対値はどうでしょうか。
「\(-3\)の絶対値は?」と聞かれたら,上の数直線から\(-3\)と原点との距離は\(3\)であることがわかるので,答えは\(3\)となります。
これらの具体例を通してわかるように,ある数の絶対値を聞かれたら,その数の符号をなくす(もしくは\(+\)にする)と良いことがわかります。
また絶対値は距離であるので,必ず\(0\)以上になります。
正負の数の大小を表現する
不等号「\(\lt\)」,「\(\gt\)」を使って,数の大小を表現
不等号「\(\lt\)」,「\(\gt\)」の使い方は小学校で学んだと思いますが,復習しておきましょう。
※不等号の使い方に自信がある人はこの説明を読み飛ばしてもらってかまいません。
「\(\lt\)」は,\(2\lt3\)のように左の数が右の数より小さいことを表します。
「\(\gt\)」は,\(3\gt2\)のように左の数が右の数より大きいことを表します。
そして,「\(\lt\)」「\(\gt\)」はそれぞれ「小なり」「大なり」と読みます。
また不等号を使うときには,\(1\lt3\gt2\)のように書いてはいけません。
この書き方だと\(1\)と\(2\)の大小がわからないからです。
そのため,3つ以上の数の大小を表すときは,\(1\lt2\lt3\),もしくは\(3\gt2\gt1\)のように不等号の向きをそろえて書きましょう。こうすることで,すべての数の大小がわかります。
不等号をそろえる向きは\(1\lt2\lt3\),\(3\gt2\gt1\)のどちらでも良いのですが,慣例的には左から右に行くほど数が大きくなるように\(1\lt2\lt3\)と書くことが多いです。
数直線上での数の大小
負の数を含んだ数直線で,数直線は上のようになることは学びましたね。
数直線上では,正の方向にある数ほど大きく,負の方向にある数ほど小さくなります。
今回の数直線でよりわかりやすくいうと,右にある数ほど大きく,左にある数ほど小さくなります。
そのため,上の数直線上で緑の点で示した\(-3,-1,+2\)の大小は\(-3\lt-1\lt+2\)となります。
しかし,いちいち数直線を思い浮かべるのは面倒と感じる人もいますよね。そこで,次の節では数直線を使わずに数の大小を求めてみましょう。
絶対値と数の大小
数直線を使わなくても数の大小がわかるようになりましょう。
例として\(-1,\dfrac{7}{3},0,-1.9,4\)の数の大小を調べたいとします。
まず,数の符号に注目してみましょう。正負の数とはで学んだように正の数は0より大きい数,負の数は0より小さい数のことでした。
そのため,まず符号を見るだけでその数が\(0\)より大きいか小さいかがわかります。
よって,下のようにおおまかな大小分けができます。\(0\)は正の数と負の数のどちらでもないことに注意です。
後は正の数のグループの数\(\dfrac{7}{3}\)と\(4\),負の数のグループの数\(-1.9\)と\(-1\)の数の大小がわかれば,全体の数の大小がわかります。
まず,正の数のグループの大小から考えていきましょう。
正の数の大小は小学校で学びましたね。
\(\dfrac{7}{3}\)と\(4\)の大小は\(4=\dfrac{12}{3}\)なので,\(\dfrac{7}{3}\lt\dfrac{12}{3}\),すなわち\(\dfrac{7}{3}\lt4\)ということがわかります。
では,小学校で習っていない負の数のグループの大小はどうでしょうか。
負の数の大小を考えるときには,その数の絶対値を考えます。
正の数では絶対値はその数自身となりますから,絶対値が大きくなるほど数が大きくなるといえるのは先ほどの例からもわかります。
負の数では正の数の場合とは反対で,絶対値が大きいほど小さくなります。
\(-1.9\)と\(-1\)の絶対値はそれぞれ\(1.9\)と\(1\)で,その大小は\(1.9\gt1\)ですね。
よって,\(-1.9\)の方が\(-1\)より絶対値が大きいので\(-1.9\lt-1\)となります。
結果として,\(-1,\dfrac{7}{3},0,-1.9,4\)の数の大小は\(-1.9\lt-1\lt0\lt\dfrac{7}{3}\lt4\)となります。
絶対値が大きいほど正の数では大きくなり,負の数では小さくなることを2-2. 数直線上での数の大小で解説したことから,なぜなのかを理解しましょう。
上の数直線は,先ほどの具体例で取り上げた数\(-1,\dfrac{7}{3},0,-1.9,4\)を赤い点で示してあります。
\(\dfrac{7}{3},4\)のように,正の数は絶対値が大きいほど数直線の右側,すなわち正の方向に行っていることがわかります。
\(-1,-1.9\)のように,負の数は絶対値が大きいほど数直線の左側,すなわち負の方向に行っていることがわかります。
したがって,絶対値が大きいほど正の数では大きくなり,負の数では小さくなります。
以上の正負の数の大小を調べる手順をまとめると次のようになります。
- 符号によって負の数,0,正の数にグループ分け
- 1 で分けたグループ内で大小比較
- 正の数\(\to\)絶対値が大きいほど,大きい
- 負の数\(\to\)絶対値が大きいほど,小さい
この手順がしっかりと身につくように例題に取り組みましょう。
例題
1. 次の数の絶対値を求めよ。
(1) \(+6\)
(2) \(-4\)
(3) \(+3.7\)
(4) \(-\dfrac{2}{5}\)
2. 次の問いに答えよ。
(1) 絶対値が\(5\)である数を答えよ。
(2) 絶対値が\(0\)である数を答えよ。
3. 次の数の大小を,不等号を使って表せ。
(1) \(-50,-70\)
(2) \(-0.6,-0.22\)
(3) \(-4,-\dfrac{7}{2}\)
4. 次の数の大小を不等号を使って表せ。
(1) \(-1,+3\)
(2)\(-5,+1,-2\)
例題1解説:絶対値を求める
1. 次の数の絶対値を求めよ。
(1) \(+6\)
(2) \(-4\)
(3) \(+3.7\)
(4) \(-\dfrac{2}{5}\)
この記事の1-1で学んだように絶対値とは「原点との距離」で,ある数の絶対値を求めるときは,その数の符号をなくす(もしくは\(+\)にする)とよいのでした。
よって,それぞれの問題の数の符号をなくしてしまえばよいので,
答えは(1) \(6\) (2) \(4\) (3) \(3.7\) (4) \(\dfrac{2}{5}\)とわかります。
例題2解説:絶対値から元の数を求める
(1) 絶対値が\(5\)である数を答えよ。
(2) 絶対値が\(0\)である数を答えよ。
3-1. 絶対値を求めるではある数が与えられて,その数の絶対値を求めました。
ここでは逆に,絶対値が与えられて,その元の数を求めることが要求されています。
まず(1)について考えましょう。絶対値は「原点との距離」なので,下の数直線で原点からの距離が\(5\)のところを考えます。
すると\(+5\)と\(-5\)の点が原点からの距離が\(5\)であることがわかります。
よって答えは\(+5\)と\(-5\)です。
※まとめて\(\pm5\)という書き方もありますが,この書き方を答案に書いてよいかは先生に確認しましょう。
(2)でも同様に考えると絶対値,すなわち,原点との距離が\(0\)である点は先ほどの数直線からもわかるように\(0\)となります。
よって答えは\(0\)です。
ここまで数直線を使って絶対値を求めましたが,1-1. 絶対値とは,数直線上での「原点との距離」で教えた,絶対値を求めるときその数の符号をなくすという考え方の逆の考え方で,絶対値に\(+,-\)の符号をつけて答えの数を求めるということもできます。
例題3解説:負の数の大小
3. 次の数の大小を,不等号を使って表せ。
(1) \(-50,-70\)
(2) \(-0.6,-0.22\)
(3) \(-4,-\dfrac{7}{2}\)
この問題では,2-3. 絶対値と数の大小で学んだ「負の数は絶対値が大きいほど数が小さい」ということを確認していきましょう。
まず(1)です。\(-50\)と\(-70\)の絶対値はそれぞれ\(50\)と\(70\)で,\(50\lt70\)となります。
よって,答えは\(-50\gt-70\)です。
次に(2)です。\(-0.6\)と\(-0.22\)の絶対値はそれぞれ\(0.6\)と\(0.22\)で,\(0.6\gt0.22\)となります。
よって,答えは\(-0.6\lt-0.22\)です。
最後に(3)です。\(-4\)と\(-\dfrac{7}{2}\)の絶対値はそれぞれ\(4\)と\(\dfrac{7}{2}\)です。通分によって,絶対値の大小が\(4=\dfrac{8}{2}\gt\dfrac{7}{2}\)とわかります。
よって,答えは\(-4\lt-\dfrac{7}{2}\)です。
例題4解説:正負の数の大小
4. 次の数の大小を不等号を使って表せ。
(1) \(-1,+3\)
(2)\(-5,+1,-2\)
2-3. 絶対値と数の大小で解説した手順を使って数の大小を調べていきましょう。
まず(1)です。\(-1\)は負の数,\(+3\)は正の数なので,答えは\(-1\lt+3\)となります。
次に(2)です。
正の数か負の数かで場合分けすると,\(+1\)は正の数,\(-2,-5\)は負の数と分けられます。
ここから,分けたグループ内で数の大小を比較すればよいので\(-2\)と\(-5\)の大小を比較していきます。
\(-2\)と\(-5\)の絶対値はそれぞれ\(2\)と\(5\)で,\(2\lt5\)となります。負の数では絶対値が大きいほど小さいので,\(-2\gt-5\)となります。
以上から,答えは\(-5\lt-2\lt+1\)となります。
\(-5\lt+1\gt-2\)のように不等号の向きがバラバラなのは,間違いなので注意しましょう。
分かりやすいように,この問題の数の数直線での位置関係も下に示しておきます。
例題の解説を全て見終わったら,練習問題にチャレンジしてみてください。
ここからは余談ですが,高校数学では\(-9\)の絶対値を\(\left|-9\right|\)と表し,数の概念をさらに広げた複素数の分野で「絶対値」の意味を改めて決定する際にも,「絶対値は原点との距離」という考え方が役に立ちます。
そのため,「絶対値は原点との距離」ということをしっかり押さえておきましょう。
例題の解答を見る
1
(1) \(6\)
(2) \(4\)
(3) \(3.7\)
(4) \(\dfrac{2}{5}\)
2
(1) \(+5,-5\)
(2) \(0\)
3
(1) 絶対値について\(50\lt70\)より,\(-50\gt-70\)
(2) 絶対値について\(0.6\gt0.22\)より,\(-0.6\lt-0.22\)
(3) 絶対値について\(4=\dfrac{8}{2}\gt\dfrac{7}{2}\)より,\(-4\lt-\dfrac{7}{2}\)
4
(1) \(-1\lt+3\)
(2) \(-5\lt-2\lt+1\)
練習問題にチャレンジ
1. 次の数の絶対値を求めよ。
(1) \(+9\)
(2) \(-11\)
(3) \(-4.5\)
(4) \(\dfrac{1}{3}\)
2. 次の問いに答えよ。
(1) 絶対値が\(3\)である数を答えよ。
(2) 絶対値が\(\dfrac{7}{5}\)である数を答えよ。
3. 次の数の大小を,不等号を使って表せ。
(1) \(-37,-23\)
(2) \(-1.3,-1.7\)
(3) \(-\dfrac{2}{3},-\dfrac{3}{2}\)
4. 次の数の大小を不等号を使って表せ。
(1) \(+4.2,-3.3\)
(2)\(-7.5,0,-9.8\)
練習問題の解答を見る
1
(1) \(9\)
(2) \(11\)
(3) \(4.5\)
(4) \(\dfrac{1}{3}\)
2
(1) \(+3,-3\)
(2) \(+\dfrac{7}{5},-\dfrac{7}{5}\)
3
(1) 絶対値について\(37\gt23\)より,\(-37\lt-23\)
(2) 絶対値について\(1.3\lt1.7\)より,\(-1.3\gt-1.7\)
(3) 絶対値について\(\dfrac{2}{3}=\dfrac{4}{6}\lt\dfrac{9}{6}=\dfrac{3}{2}\)より,\(-\dfrac{2}{3}\gt-\dfrac{3}{2}\)
4
(1) \(+4.2\gt-3.3\)
(2) \(-9.8\lt-7.5\lt0\)







