例題を解く前に，割り算における「商」と「余り」について，例を用いて説明します。

例えば，\(4 \div 2\)という割り算を行う際，考え方としては次の図のように\(4\)個のものを\(2\)個ずつ分けるときに何組できるか？という考え方になります。

この場合は\(2\)組に分けられるので，答えは\(2\)となります。この答えの\(2\)のことを，割り算における「商」と呼びます。このように余りが発生せずに丁度分けられる場合が「割り切れた」状態ということになります。

それに対し，\(5\div 2\)という割り算を行う際，同じように考えると，\(5\)個のものを\(2\)個ずつに分けるとき，\(2\)組出来ますが\(1\)個余った状態になります。

この場合，完成した\(2\)組の\(2\)が「商」となり，余りが\(1\)個という事になります。このように余りが発生する場合が，「割り切れない」状態ということになります。

それでは，「商」と「余り」について理解できたところで今回の問題である\(13\div 5\)の計算を行いましょう。

考え方としては\(13\)個のものを\(5\)個ずつ分けるとき，何組出来て何個余るか？という意味になります。つまり次の図のように\(5\)個ずつの組は\(2\)組できて，余りが\(3\)個となりますので，

この問題の商は\(2\)，余りは\(3\)ということになります。これが割り算の基本的な考え方です。

次に，別解として筆算を用いて計算する方法について説明します。例題1を筆算で表すと次のようになります。

①②の順に，十の位から計算を行っていきます。まず，割られる数の\(13\)の十の位の「\(1\)」と，割る数「\(5\)」についての比較をします。割る数「\(5\)」の倍数で，「\(1\)」以下になる数を探します。

この場合，\(5 \times 1=5\)となり，この時点で「\(1\)」を越えてしまっているので，「\(1\)」より小さい数は\(5 \times 0=0\)しかないことになります。

よって，「\(0\)」を割られる数の上に書き，これが商の十の位の数字になります。次に矢印のように，\(0 \times 5\)を計算し，答えの\(0\)を\(1\)の下に書きます。

そして，上から下に引き算を行うと，\(1\)となります。次に②の一の位の\(3\)を真下に下ろします。

今度は割られる数の\(13\)と割る数\(5\)についての比較をしますが，同じ手順ですので解説は省略します。割り算の筆算はこの一連の流れを各位で繰り返すことで，「商」と「余り」が求まります。

ちなみに，\(0\)の計算部分については，実際には省略をするのが普通のため、以後の解説では省略します。

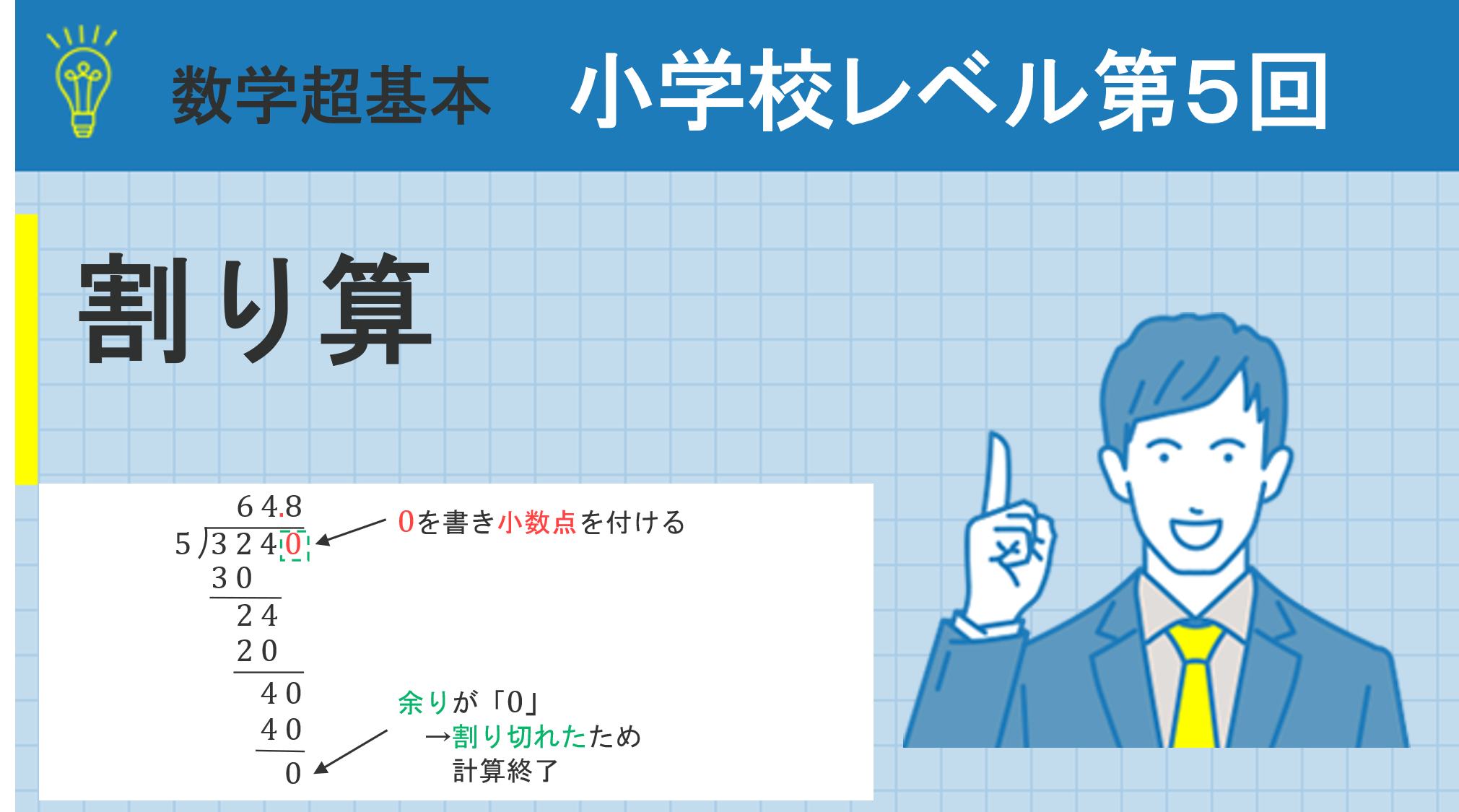
普通に計算しただけでは「余り」が出てしまいましたね。今回は「割り切れるまで計算しなさい」という条件が付いているので，余りが\(0\)になり割り切れるまで計算しましょう。

\(324\)は\(5\)の倍数ではないため割り切れませんが，この問題では割り切れるまで計算するという条件が付いているので，次のように小数の範囲まで拡げて計算を行い，割り切れるまで計算します。

次の問題は，割られる数\(3\)に対し，割る数\(150\)の方が桁数が多いため，このままでは筆算を行うことが出来ません。

このように，割る数よりも割られる数の桁数が少ない場合，商の部分に\(0\)を書き，小数点を打ちます。そして割られる数\(3\)に\(0\)を付けたし，割る数と桁数を合わせます。そして整数の割り算と同じように計算を行っていきます。

割られる数に対し，割る数の桁数が多いときは，桁数を合わせ整数の割り算と同じように計算

小数が含まれた筆算を行う場合，小数のままでは計算を行わず，割られる数と割る数が整数になるように\(10\)倍していきます。この問題の場合，\(8.4\)と\(4.2\)に\(10\)を掛けると整数になるので，\(10\)倍して整数の状態にし，\(84 \div 42\)の割り算を行います。

小数を含む割り算では、小数が整数になるまで10倍していき、整数に直した状態で計算する

この3問も先ほどと同じく小数が含まれた問題です。そのため小数を整数に直した状態で計算するようにしましょう。

例題2.(8)～(9)は，割る数と割られる数の一の位や十の位が\(0\)になっています。このような場合は，計算を楽にするために，小数にならない範囲で\(10\)や\(100\)で割ってから計算を行うようにします。

割る数と割られる数の一の位や十の位が\(0\)になっているときは，小数にならない範囲で\(10\)や\(100\)で割ってから計算を行う

以上，割り算の筆算の解説でした。これで，どんな問題でも解くことができるようになると思います。復習のためにも練習問題にチャレンジすることをおススメします。