まずは単位とは何なのかについて理解しましょう。

単位とは「ものの量をはかるための基準として定められた量」

そもそも単位とは、「ものの量をはかるための基準として定められた量」です。もし単位が無い世界だとこんなことが起きるかもしれません。

小学生A「Bくんは家から学校までどれ位歩くの？」

小学生B「たくさん歩くから遠いと思うよ」

小学生A「それだと具体的にどれ位歩くのか分からないね」

小学生B「ん～でも何て表現すれば伝わるのか分からないなぁ」

これが単位のある世界だとBくんは具体的に返事することができます。

小学生B「家から歩いて\(2\mathrm{\,km}\)で\(25\)分かかるよ」

小学生B「そうなんだ。遠くて大変だね。」

このように、単位が無いと困ることがたくさんあります。だから私達は，ものの量をはかる基準として「単位」という量を定めて使っているのです。

基準となる単位

今回の例題では，基準となる単位は次の3つだけしか使っていません。この3つの単位は日常生活で利用することが特に多いと思います。

次に単位の前に書くアルファベットについて説明します。

基準の単位だけでは \(0\)（ゼロ）が増えてしまうので不便

基準の単位だけでは，とても大きい量や，とても小さい量を表現しようとしたとき，\(0\)（ゼロ）をたくさん書かないといけません。例として以下に書きましたが，\(0\)（ゼロ）が多すぎて間違えしてしまいそうですね。

アルファベットを前に付けてケタ数を表現

上記のままだと実用上不便なので，基準となる単位のケタ数を表すために，次のようなアルファベットを単位の前に書くことができます。

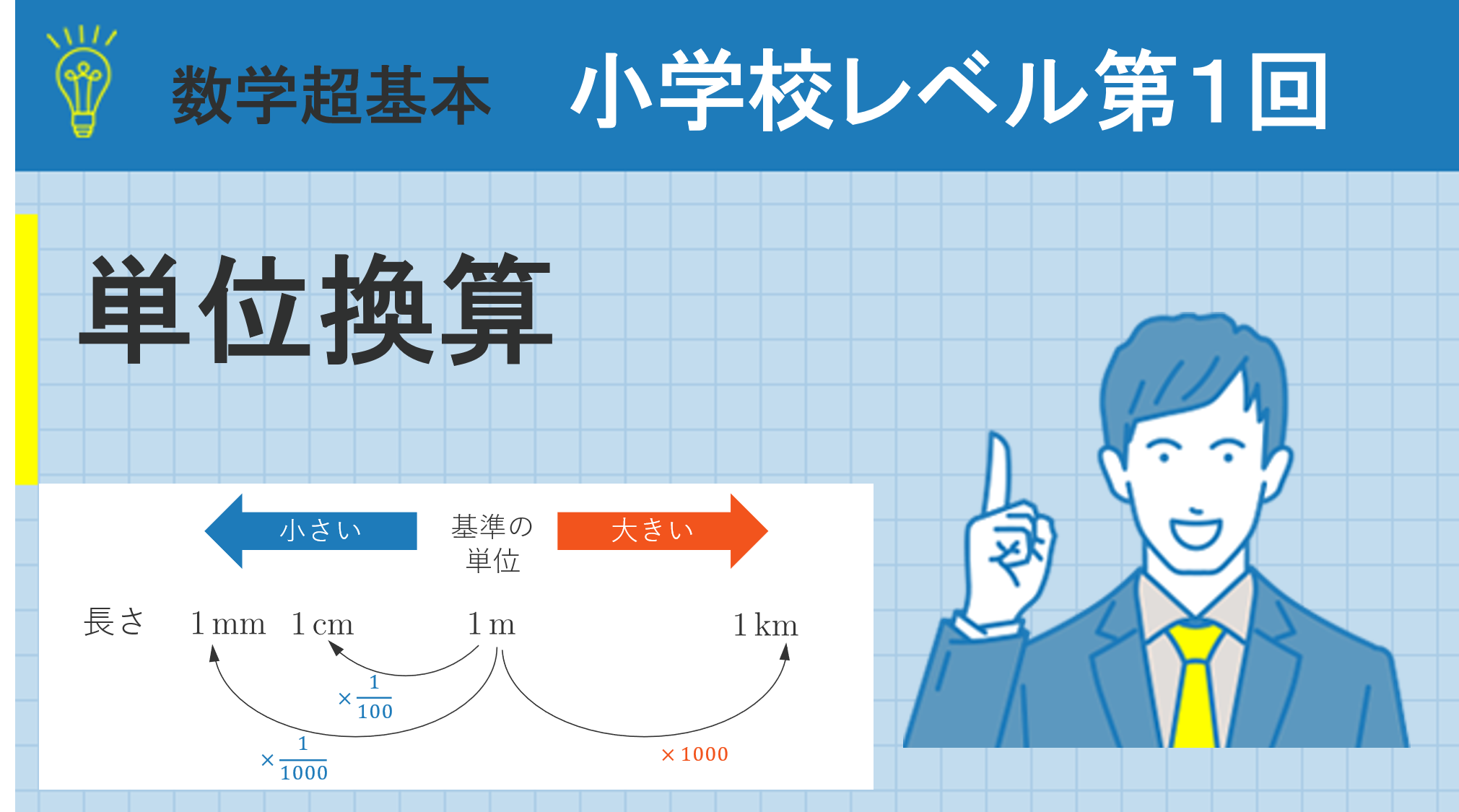
単位換算ではこのアルファベットを使い，別の単位で表した数値を求めます。例えば長さを表す\(1\mathrm{\,m}\)(メートル)は，\(1000\)倍の量をもつ\(\mathrm{\,km}\)(キロメートル)に単位換算すると\(0.001\mathrm{\,km}\)(キロメートル)となります。

基準となる単位とケタ数の関係

基準となる単位とケタ数の関係をまとめます。なお重さだけは\(1\mathrm{\,kg}\)の\(1000\)倍の量として\(\mathrm{t}\)(トン)があります。

気づいた人もいると思いますが，上の図では\(\mathrm{h}\)(ヘクト)や\(\mathrm{da}\)(デカ)を書いていませんね。それに\(\mathrm{c}\)(センチ)を使っているのは「長さ」だけです。

この理由は，あくまで上の図は世の中で使われている単位を書いたものだからです。しかしアルファベットはケタ数を表すものなので，例えば次のような単位換算をおこなっても間違いではありません。

しかし，これらは一般的に使われていない単位になります。もし使ったしても他の人に伝わらないかもしれませんので，使わないようにしましょう。