対称性は体積問題に限らず，他の問題でも重要なテクニックです。

なぜなら対称性を考えることにより，考える範囲を小さくすることができるからです。

体積問題においては，左右対称という言葉のように，対称性とは鏡写しの状態というイメージを持ちましょう。
※この鏡写しの対称性は鏡像対称性と呼ばれ，実際は対称性の一部になります。

原点中心の半径\(1\)の球（以降\(\mathrm{B}\)と呼ぶことにします）の体積を考えることで，対称性を理解しましょう。

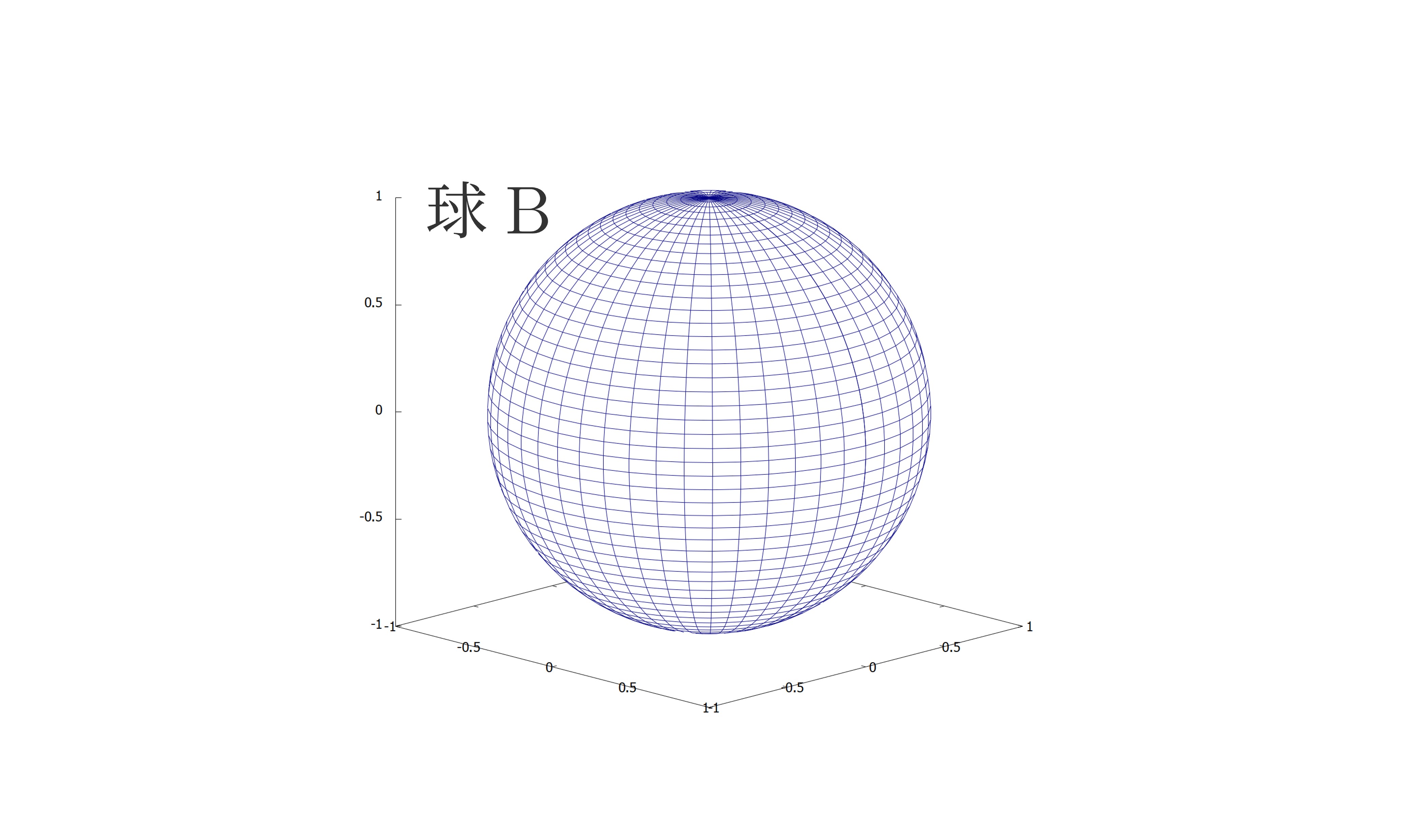
球\(\mathrm{B}\)の方程式は

\(x^{2}+y^{2}+z^{2}=1\)

となりますね。

この式で\(x\)を\(-x\)に置き換えたとしても，式自体は不変です。

これは球\(\mathrm{B}\)が\(yz\)平面に関して対称だということを表します。

つまり\(yz\)平面を鏡として考えると，球\(\mathrm{B}\)の\(yz\)平面の上の部分\(\mathrm{B_{1}}\,(x\geqq 0)\)と下の部分\(\mathrm{B_{2}}\,(x\leqq 0)\)が鏡写しになっているということですね。

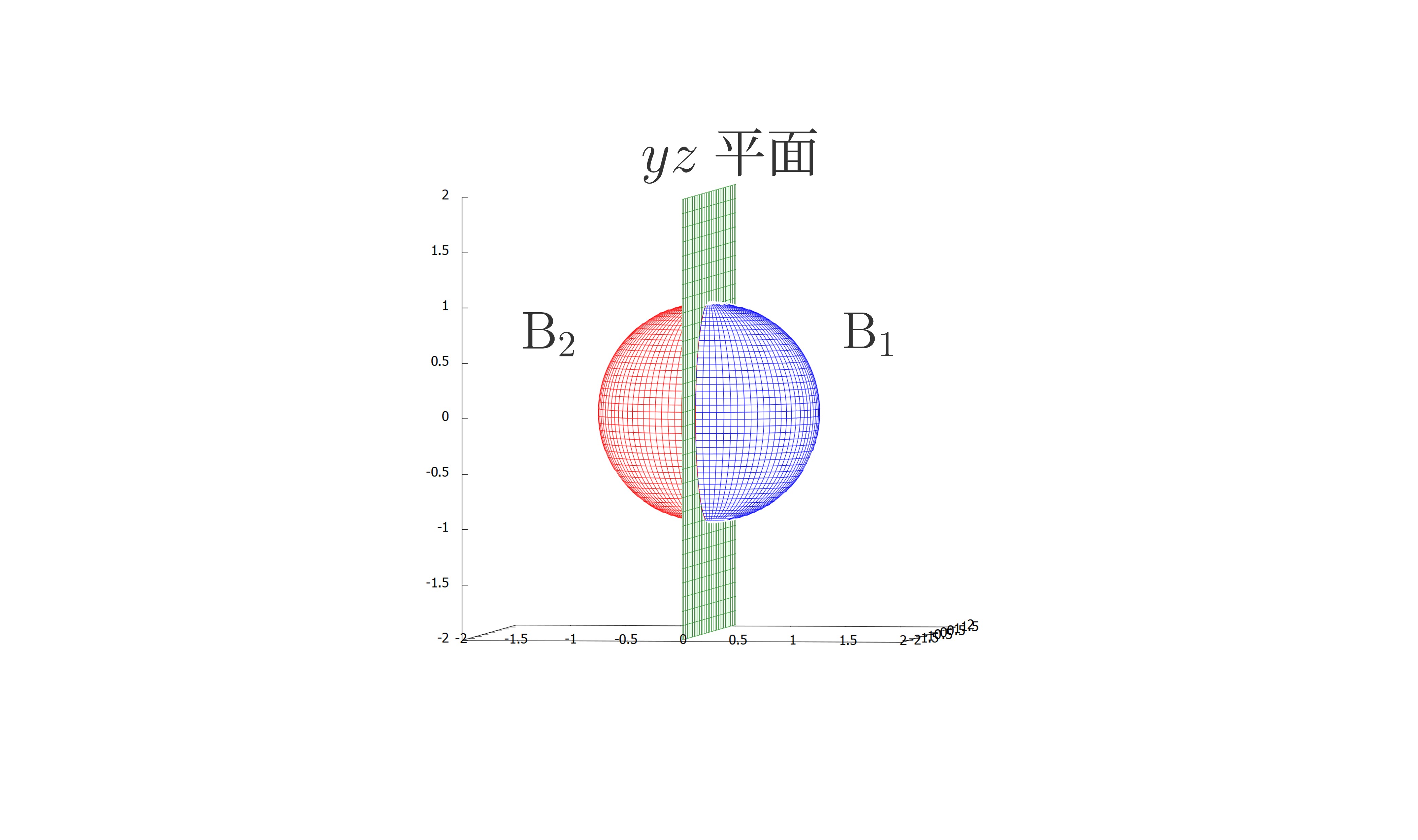
鏡写しなので\(\mathrm{B_{1}}\)と\(\mathrm{B_{2}}\)の体積は等しく，\(\mathrm{B}\)の体積は\(\mathrm{B_{1}}\)（もしくは\(\mathrm{B_{2}}\)）の\(2\)倍だと言えます。

そのため\(\mathrm{B}\)の体積を求めたいなら，\(\mathrm{B}\)より小さい\(\mathrm{B_{1}}\)の体積を考えるだけで済むということです。

このように対称性を利用して，\(\mathrm{B}\)から\(\mathrm{B_{1}}\)へと考える範囲を小さくすることができました。

これが対称性の利点です。

入試において時間を節約するためにも，対称性を見つけることは常に意識しておくようにしましょう。

ただし対称性について，この解説ほど詳しく書く必要はないので，答案では「対称性より」でOKです。

対称性をはっきり使う問題としては東大数学の体積問題が解けるようになろう！　その１で挙げた東大2005年度理系問6が挙げられます。

この問題の解説は，上で紹介した記事に解答PDFとしておいてあるので，ぜひ参考にしていってください。

円錐を表す方程式は高校数学では習いませんが，高難度の入試だと必要になる，もしくは知っておくと，解答が書きやすくなります。

例えば東大2017年度理系問6，2013年度理系問6，2020年度理系問5，京大2020年度理系問6などで役立ちます。
※京大2020年度理系問6に関しては円錐ではなく回転体の方程式を利用しますが，考え方は同じなので紹介させていただきました。

ただし，ここで紹介するのはあくまで円錐の「側面の」方程式で，底面まで含めた本当の円錐の方程式ではないです。しかし，ここでは「円錐の側面の方程式」を「円錐の方程式」と書かせていただきます。

円錐の方程式は次の2つのどちらかの方法で作りましょう。

1. ベクトル方程式から導出
2. 断面の方程式から導出

円錐の方程式は高校数学で習わないため，少なくともどちらかの導出は書きましょう。

それでは，それぞれの導出について解説していきたいと思います。

ベクトル方程式から導出

底面が\(xy\)平面に位置する半径\(1\)の原点中心の円で，頂点が\((0,0,1)\)に位置する円錐\(\mathrm{C}\)の方程式を導出してみましょう。

主にベクトルの内積によって導出している点がポイントです。

導出のために原点を\(\mathrm{O}\)，頂点を\(\mathrm{A}\)とおきます。

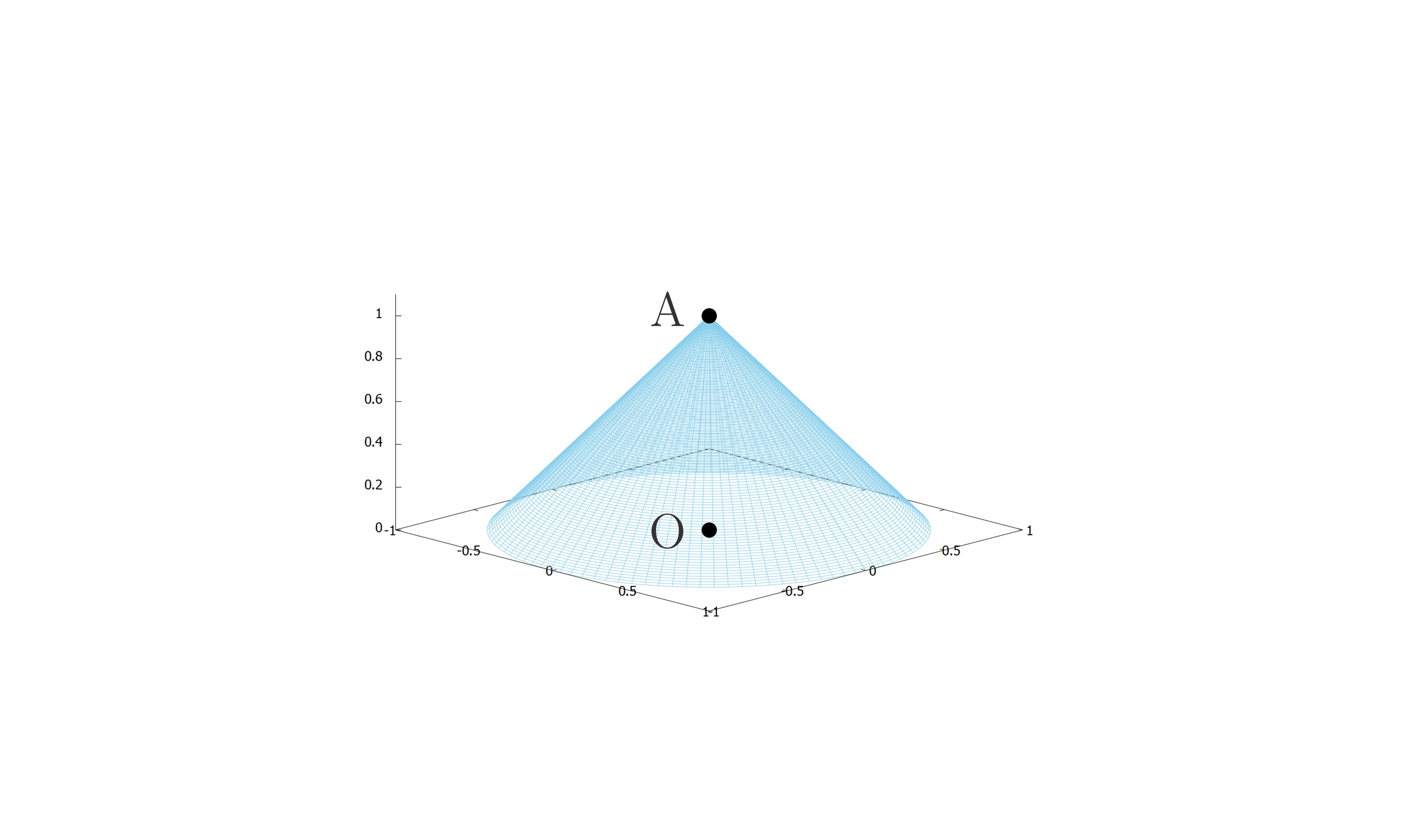
図形の方程式を導く際は，その図形上の点を\((x,y,z)\)とおいて，それらの座標が満たす方程式を導出すればよいですね。

そこで円錐\(\mathrm{C}\)上の点を点\(\mathrm{P}\,(x,y,z)\)とおいて，この点\(\mathrm{P}\)が満たす方程式を考えます。

すると\(\overrightarrow{\mathrm{AP}}\)と\(\overrightarrow{\mathrm{AO}}\)のなす角度が常に\(45^{\circ}\)であることが分かります。

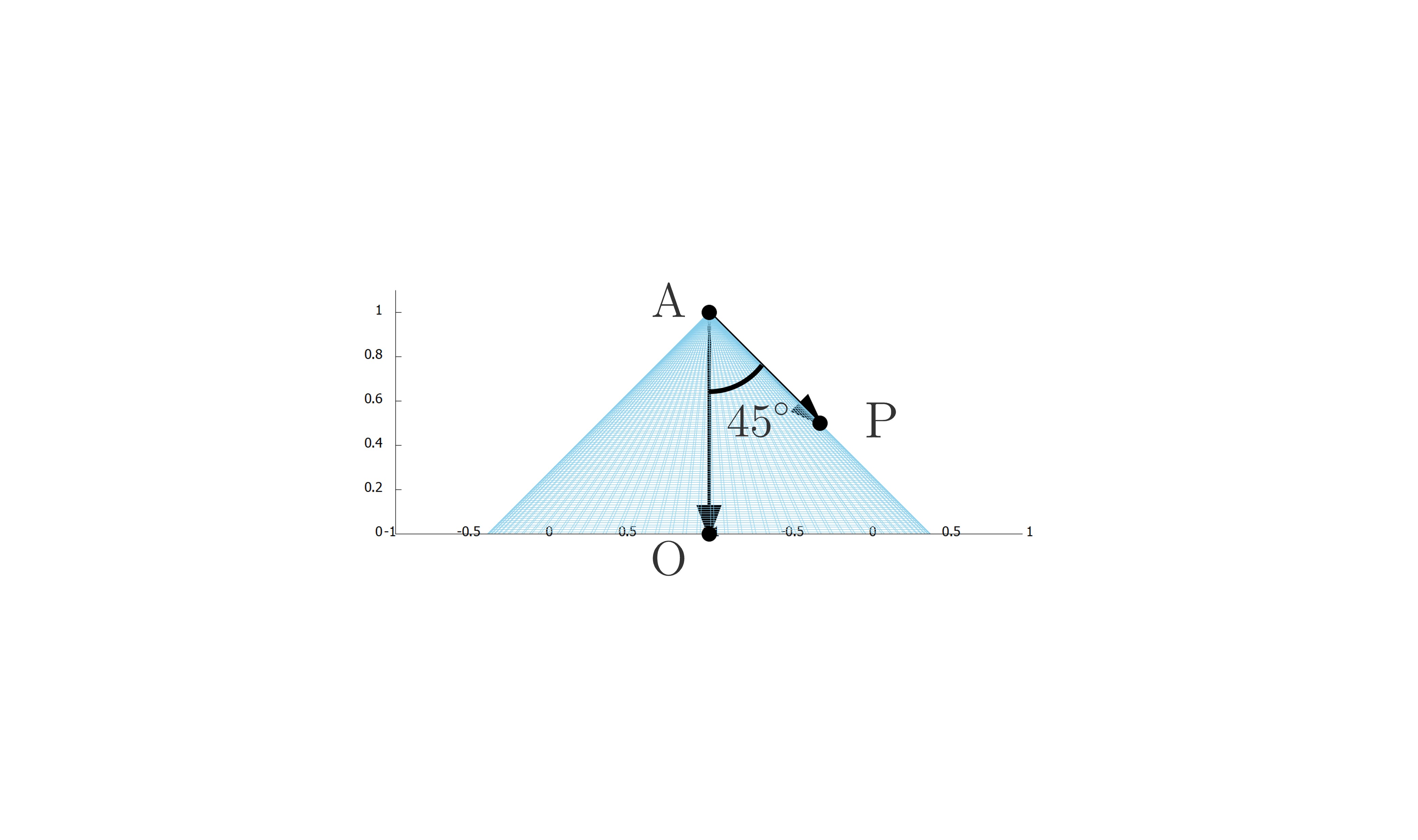
つまり
\(\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{\mathrm{AO}}=|\overrightarrow{\mathrm{AP}}||\overrightarrow{\mathrm{AO}}|\cos45^{\circ}\)
が成り立ちます。

\(\overrightarrow{\mathrm{AP}}=(x,y,z-1),\,\overrightarrow{\mathrm{AO}}=(0,0,-1)\)ですから，この方程式は

となります。

しかし，この方程式の表す図形は

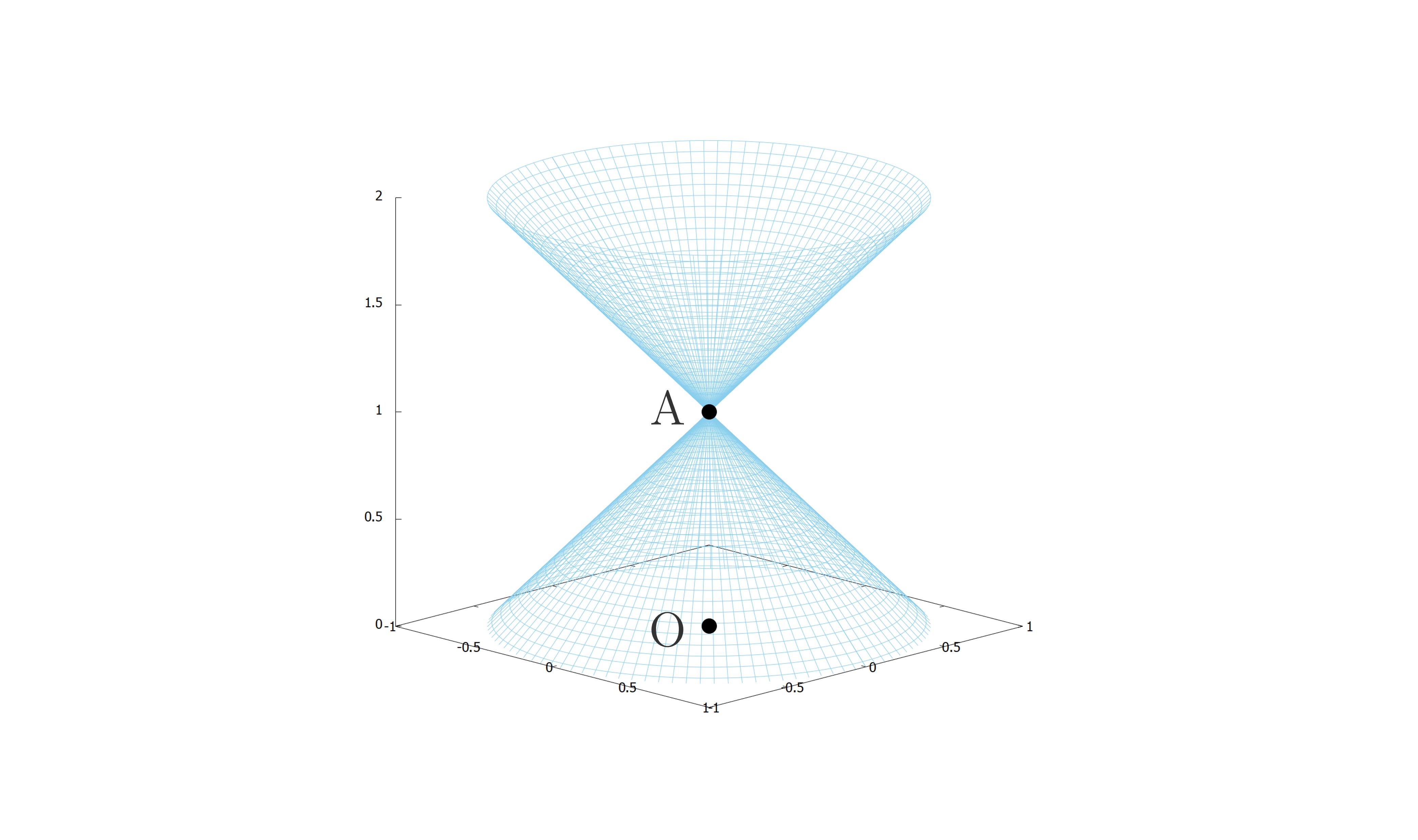
のように，円錐\(\mathrm{C}\)より大きい領域を表すため，さらに条件をかける必要があります。

そのため，さらなる条件として，円錐\(\mathrm{C}\)上の点はすべて\(0\leqq z\leqq 1\)の範囲にあることを用います。

よって円錐\(\mathrm{C}\)の方程式は

と求められます。

この導出は次に紹介する導出に比べ，導出しやすいというメリットがある一方，考え方が円錐にしか使えないという適用範囲の狭さのデメリットがあることを覚えておきましょう。

• 主にベクトルの内積によって導出

断面の方程式から導出

次に断面の方程式から先ほどの円錐\(\mathrm{C}\)の方程式を導出してみましょう。

こちらは断面での方程式を考える\(\to xyz\)空間での方程式に拡張するという流れで導出します。

円錐\(\mathrm{C}\)を平面\(z=t\)（\(t\)は定数）で切った時の断面を考えます。

円錐\(\mathrm{C}\)は明らかに\(0\leqq z\leqq 1\)にあるので，\(0\leqq t\leqq 1\)での断面を考えれば十分ですね。

円錐\(\mathrm{C}\)を平面\(z=t\)で切った時の断面は円になるので，その中心と半径を求めれば円の方程式が求まります。

円の中心は\(z=t\)を線分\(\mathrm{OA}\)との交点なので\((0,0,t)\)だと分かります。

また半径は\(zx\)平面を切り取った下図の相似比から，\(1-t\)だと分かります。

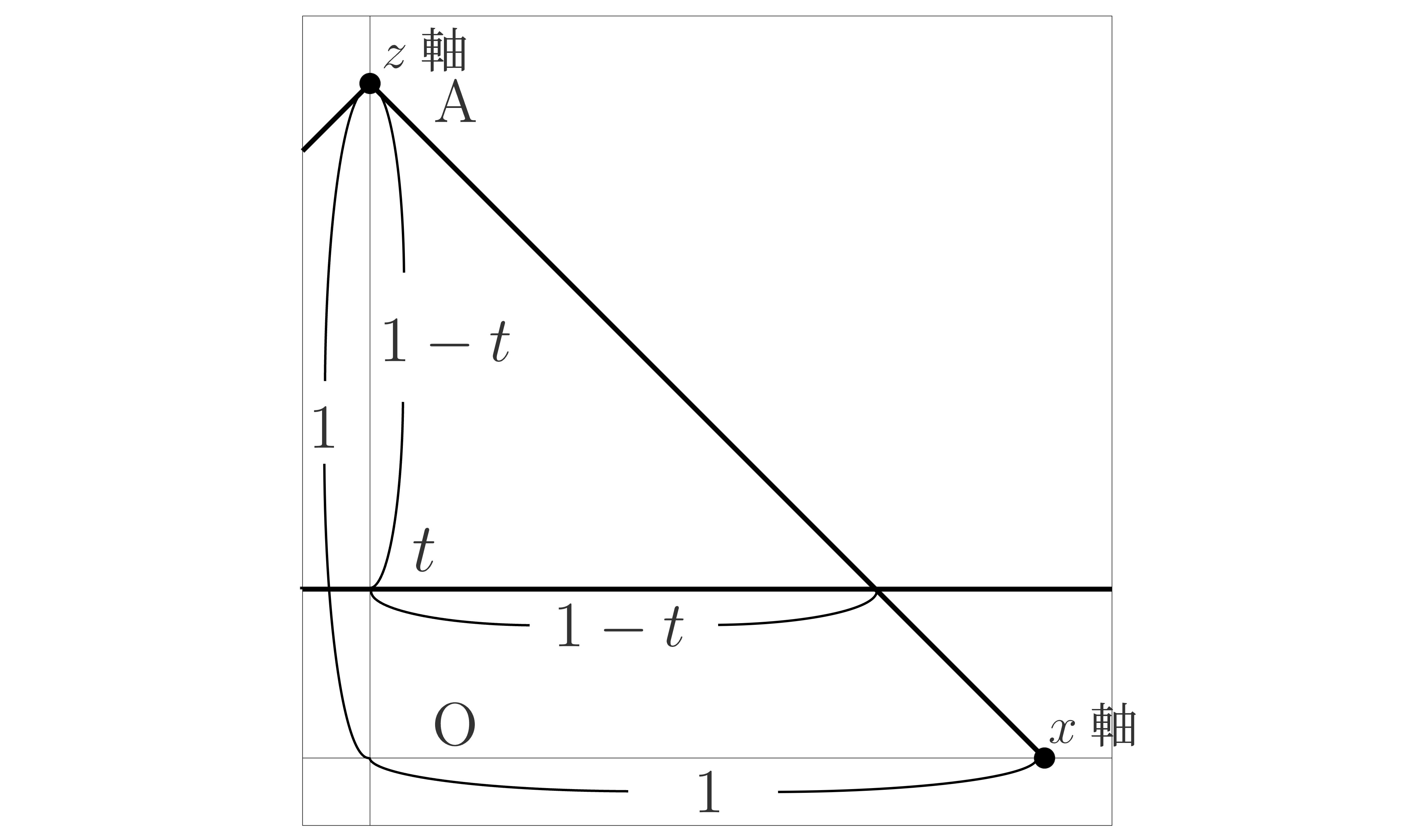
つまり\(z=t\)による断面の方程式は

\(x^2+y^2=(1-t)^2\)

だと分かります。

\(t\)を\(z\)で置き換えることにより，円錐\(\mathrm{C}\)の方程式は

と求められます（\(0\leqq t\leqq 1\)に注意しましょう）。

同じような考え方をすることで，円錐のみならず回転体の方程式を求めることができます。

実際に京大2020年度問6ではこの考え方をもとに回転体の方程式を求め，解いていくことができます。

こちらの導出は前の導出に比べ，回転体まで同じ考え方が使えるというメリットがある一方，導出が面倒な場合があるというデメリットも持つことを覚えておきましょう。

• 断面での方程式を考える\(\to xyz\)空間での方程式に拡張

媒介変数表示

円錐の方程式を\(x,y,z\)の関係式ではなく，媒介変数を用いて表示することで問題が解きやすくなる場合があります。

例えばで解説した東大2020年度理系問5がまさにそれです。

先ほどの円錐\(\mathrm{C}\)の方程式は

のように，\(\theta\)を媒介変数にして表すことができます。

「断面の方程式から導出」で，平面\(z=t\)上の断面が半径\(1-t\)の原点中心の円を表していたことを考えると，この表示を解釈しやすいです。

つまり，円錐を\(z\)座標によって半径が変化する円の連なりと考えているわけです。

繰り返しになりますが円錐の方程式を媒介変数で表示することで，東大2020年度理系問5のように解答しやすくなる場合があります。

しかし，媒介変数表示はそれほど使う場面が多いわけではありませんので，頭の片隅に入れておく程度で十分です。

体積問題で役立つ対称性，円錐の（側面の）方程式について理解していただけたでしょうか。

自信のない方はここで紹介した問題を解いてみることをオススメします。

これらの問題は東大や京大といった難関大の問題のため，完璧に解答できることよりも，ここで学んだ方針に従った解答が書けていたら十分です（そのため解けなくても自信を無くさないようにしましょう）。

これまでに私はLESSON1，LESSON2，LESSON3と，このおまけの記事で体積問題を解説して参りました。

もしもこれらの記事をすべて読んでくれている方がいたら，著者としましてはとてつもなく嬉しく，感謝を申し上げたいと思います。

ここまで読んでいただきありがとうございました。